Excel Quantile berechnen: Perzentile, Dezile und Co und der Unterschied zwischen .exkl und .inkl
Zur Berechnung von Quantilen in Excel gibt es viele Missverständnisse. Quartile lassen sich mit der entsprechenden Formel =quartile leicht berechnen. Allerdings gibt es seit 2010 dort zwei Varianten. Noch unklarer ist die Berechnung von Dezilen oder Perzentilen. Hier liest man manchmal, das sei nur auf dem Umweg über eine Quartilsberechnung möglich. Was allerdings falsch ist.
Zur Erinnerung: Was sind Quantile
Zur Erinnerung: Quantile unterteilen einen Datensatz in mehrere möglichst gleich große Teilgruppen. Bei einem Quartil (Quartil mit r, nicht mit n wie Quantil) sind das vier gleich große Gruppen, bei einem Quintil fünf, bei einem Dezil zehn und so weiter.
Die Quantilswerte sind jeweils die Grenze. Deshalb gibt es bei einem Quartil drei Werte, nämlich die Grenze vom unteren Viertel zum zweiten, vom zweiten zum dritten und vom dritten zum obersten.
Beispielsweise lässt sich mithilfe der Perzentile berechnen, ab welchem Einkommen jemand zum obersten 1,0 Prozent der Bevölkerung gehört. Der Ökonom Thomas Piketty hält solche Werte für deutlich besser, um beispielsweise die Entwicklung der Ungleichheit zu beschreiben als synthetische Indikatoren wie den Gini-Koeffizienten.
Quantile mit Excel rechnen
Es gibt viel Unwissen im Netz über die Berechnung von Quantilen mit Excel. Chip, der erste Treffer bei meiner Recherche, behauptet in einem Praxistipp beispielsweise, nur Quartile ließen sich problemlos in Excel berechnen, Perzentile dagegen sich nur als Bruchteile von Quartilen berechnen.
Der Beitrag enthält aber gleich mehrere Fehler. Wahr ist nur, dass es neben der für alle Quantile geltende Formel eine besondere Formel für Quartile gibt. Davon abgesehen ist so ziemlich alles falsch oder veraltet. So wird dort die veraltete Formel =quartile(;) verwendet statt der aktuellen Formen =quartile.ink(;) und =quartile.exkl(;). Beide neue Formeln berechnen Quartile, auf den Unterschied in der Berechnung komme ich gleich zu sprechen.
Außerdem ist es falsch, dass man einfach einen Bruchteil eines Quartils berechnen müsse. Der Gedanke ist naheliegend, dass das 1. Quartil das 25. Perzentil sei und man daher in der Formel statt einer 1 eine 1/25 schreiben müsse. Funktioniert aber nicht.
Formeln für Quartile und Quantile
Dabei ist die Sache zunächst ganz einfach. Es gibt eine Formel für Quartile und eine zweite, mit der ich alle Quantile berechnen kann, neben Quartilen also beispielsweise auch Quintile (fünf Gruppen), Dezile (10 Gruppen) und Perzentile (100 Gruppen).
Bei den Quartilsformeln muss ich in der Klammer zunächst den Datenbereich angeben, dann die Nummer des Quartils. Also eine 1 für das erste Quartil, eine 2 für das zweite (das auch der Median ist) und eine 3 für das Dritte.
Die Quantilsformeln funktionieren genauso, allerdings muss ich bei der Zahl hinter dem Strichpunkt noch angeben, in wie viele Gruppen ich meine Daten einteilen will. Bei Quartilen sind das 4. Ich könne Quartile als auch mit den Quantilsformeln berechnen, müsste hinter dem Strichpunkt für das 3. Quartil statt einer 3 aber 3/4 schreiben. Eine 3, weil ich das 3. Quantil suche und eine 4, weil ich Quartile verwende. Beim 3. Perzentil würde dort 3/100 stehen.
Warum gibt es verschiedene Quartilsformeln
Allerdings kennt Excel jeweils zwei Formeln für Quartile und für Quantile, nämlich
quartile.exkl(;) und quartile.inkl(;) sowie
quantil.exkl(;) und quantil.inkl(;).
Wer Quantile berechnen will, muss sich zunächst klar darüber werden, wie er seine Daten unterteilen will. Will ich gleich große Gruppen bilden, bei Quartilen also vier Gruppen mit je gleich vielen Fällen? Dann brauche ich die Formel mit .exkl. Oder will ich das ein Viertel der Fälle unter dem ersten Quartil liegt und drei Viertel darüber? Dann brauche ich .inkl.
Aber warum ist das überhaupt ein Unterschied? Weil die Quantilswerte selbst ja keiner Gruppe angehören. Sehen wir uns das an einem Beispiel an.
Schauen wir uns das mal genauer an
Ich habe ein Beispiel mit 13 Werten gewählt. Die oberste Zeile ist die laufende Nummerierung, die untere mein eigentlicher Wert. Sagen wir mal, es ist die Zahl der Fehler in einer Klausur. Die Daten sind, wie man sieht sortiert, vom besten Ergebnis (zwei Fehler) bis zum schlechtesten (17 Fehler).
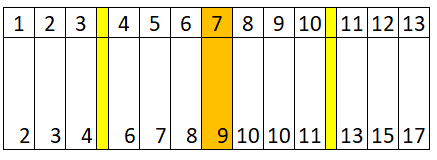
Wir sehen, dass wir vier Gruppen mit je drei Werten haben. Unser erstes Quartil liegt zwischen dem dritten und dem vierten Wert, wir nehmen deshalb die Mitte aus beiden Werten, also 5. Wie wir das bei größeren Datenmengen von Hand berechnen, erkläre ich unten. Wir haben also vier Gruppen mit je drei Werten, wobei die Quartile selbst nicht mit dabei sind.
Die Bedingung, dass drei Viertel der Werte über dem 1. Quartil liegen sollen gilt nur, wenn wir die Quartilsgrenzen – hier nur der siebte Wert – nicht mitzählen, ihn also exkludieren. Deshalb heißt die Formel in Excel auch =quantil.exkl.
Wenn ich Quartile habe, kann ich sowohl die Formel quantil.exkl als auch quartile.exkl (mit r und einem e vor dem Punkt) benutzen, bei allen anderen Quantilen nur quantil.exkl. Wie genau das geht, erkläre ich gleich.
Die Formel =quantil.inkl
Das sieht auf den ersten Blick ganz gut aus, hat aber auch einen Nachteil. Jetzt liegen drei Werte unter meinem ersten Quartal und zehn darüber, also mehr als dreimal so viele. Zumindest, wenn ich den siebten Wert inkludieren.
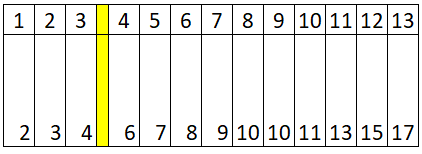
Nehme ich statt der Mitte aus dem dritten und vierten Wert den vierten Wert selbst als 1. Quartil, liegen dagegen genau drei Werte darunter und neun darüber, also ganz genau dreimal so viele. Richtig, die Formel für diesen Ansatz heißt in Excel deshalb =quantil.inkl beziehungsweise – wieder nur bei Quartilen – quartile.inkl.
quartile.inkl oder quartile.exkl – Welche Formel ist die bessere?
Ich muss mich also entscheiden, welchen Ansatz ich wähle. Bei 13 Werten ist der Unterschied nicht so groß, hätten wir elf, wäre der dritte Wert unser 1. Quartil. Dann wäre das Missverhältnis mit der ersten Formel noch extremer, es lägen mit der ersten Formel zwei Werte unter dem 1. Wert und acht darüber, also dreimal so viele.
Dafür sind meine einzelnen Gruppen jetzt unterschiedlich groß. Mein 1. Quartil ist der 4. Wert, das 2. Quartil(der Median) ist der 7. Wert und das 3. Quartil ist der 10. Wert. Meine zweite Gruppe umfasst also nur zwei Personen, ebenso die vierte.
Excel hat in der alten Variante übrigens ausschließlich die zweite Variante (=quantil.inkl beziehungsweise =quartile.inkl) verwendet. Mir persönlich ist diese Variante auch näher.
Es hängt auch ein bisschen davon ab, was man ausweisen möchte. Wollen wir eine Aussage treffen wie „Das reichste Prozent (also das reichste Perzentil) der Bevölkerung hat einen Anteil von … am Einkommen“, dann ist die Formel quantil.inkl intuitiver, stelle ich alle 99 Perzentile dar ist es schwieriger sich zu entscheiden.
„Risikohinweis!“
Ich muss zur Sicherheit sagen, dass ich mich hier nicht auf offizielle Angaben von Microsoft stütze. Die Hilfe macht nämlich zum Unterschied zwischen den Varianten mit .exkl und .inkl keine Angaben. Aber ich habe meine Hypothese, die ich hier dargestellte habe, natürlich mehrfach getestet. Mehr dazu im Kapitel „Für alle, die es genau wissen wollen“.
Quartile und Quantile in Excel berechnen
Wir müssen jetzt nur noch eine Kleinigkeit klären, nämlich welche Daten in die Formel eingegeben werden müssen.
Die Formel für Quartile
Bei Quartilen ist die Sache ganz einfach. Zunächst wird der Datenbereich markiert. Stehen meine Daten in den Zellen A2 bis A14 beginnt meine Formel also mit =quartile.inkl(A2:A14;…) – oder =quartile.exkl(A2:A14;…), wenn ich die erste der oben vorgestellten Varianten verwenden will.
Aber was seht nach dem Strichpunkt? Das ist ganz einfach. Suche ich das erste Quartil eine 1, für das zweite eine 2 und für das dritte eine 3. Bei der alten Formel =quartile(…;…) – also ohne den Zusatz .inkl oder .exkl – gibt es noch die Möglichkeit eine 0 für das Minimum und eine 4 für das Maximum einzugeben. Bei der neuen Formel gibt es das nicht mehr, aber dafür gibt es ja die Formeln =max() und =min().
Die Formel für Quantile
Bei den Formeln für Quantile ist es etwas schwerer, aber nicht viel. Auch hier muss ich den Datenbereich angeben. Hinter dem Strichpunkt schreibt man am einfachsten einen Bruch. Oben im Bruch steht das gesuchte Quantil, also das erste, zweite und so weiter.
Unter dem Bruch steht die Anzahl der Gruppen, also 4 bei Quartilen, 5 bei Quintilen und so weiter. Suche ich das erste Quartil steht da also 1/4, für das dritte Dezil 3/10 und für das 99. Perzentil 99/100. Natürlich kann man auch eine Dezimalzahl schreiben, statt 1/4 also 0,25. Aber ich finde einen Bruch einfacher.
Stellen wir uns eine ganz einfache Datenreihe vor. Sie besteht aus elf Zahlen von 1 bis 11. Nehmen wir einfach an, das wäre das Taschengeld von Kindern, vom Kind mit dem niedrigsten bis zum Kind mit dem höchsten Taschengeld. Die linke Spalte ist die laufende Nummer, die mittlere der Name und die rechte Spalte das Taschengeld. Hans und Hermine bekommen also kein Taschengeld, Marianne dagegen 10,- Euro.
Ein Beispiel
Wir haben einen Datensatz der von A1 bis A2524 reicht. Weil ich Perzentile berechnen will, brauche ich die Formel die mit =quantil. beginnt. Zuerst muss ich mich für eine Variante entscheiden. Ich finde die zweite Variante intuitiver bei der ein
Hundertstel der Daten über dem 99. Perzentil liegt und 99 Hundertstel darunter. Also verwende ich die Formel =quantil.inkl(). Ich interessiere mich aktuell nur für das 99. Perzentil.
Weil die Daten in den Zellen A1 bis A2524 stehen, schreibe ich
=quantil.inkl(A1:A2524;99/100). Würde ich das erste suchen, stände da
=quantil.inkl(A1:A2524;1/100), interessierte ich mich für das zweite Quartil
=quantil.inkl(A1:A2524;2/4). Oder im letzten Fall auch =quartile.inkl(A1:A2524;2).
Für alle die es ganz genau wissen wollen
Wie gesagt macht Microsoft keine Angaben zur Berechnung. Wie habe ich also untersucht, wie die Formel funktionieren und welche mathematischen Formeln stehen hinter den Excel-Formeln?
Hier haben wir eine Tabelle, die praktischerweise schon sortiert ist. Das ist sinnvoll, wenn ich die Berechnung händisch durchführen will.
| lfd. Nr. | Name des Kindes | Taschengeld |
| 1 | Hans | 0,- |
| 2 | Hermine | 0,- |
| 3 | Xaver | 1,- |
| 4 | Beat | 2,- |
| 5 | Hildegard | 3,- |
| 6 | Clotilde | 3,50 |
| 7 | Tusnelda | 4,- |
| 8 | Ambrosius | 4,- |
| 9 | Sigismund | 5,- |
| 10 | Helene | 7,- |
| 11 | Marianne | 10,- |
Was rechnet Excel bei den Formel =quantil.exkl und =quartile.exkl?
Berechnen wir zunächst mal Quartile für die Formeln mit dem Zusatz .exkl, das ist einfach. Oder noch einfacher, erst den Median, also den Wert, der unsere Gruppe in genau zwei gleich große Gruppen teilt. Bei 11 Werten ist deshalb der sechste Wert der Median, fünf Werte sind kleiner, fünf sind größer. Dafür können wir auch die Median-Formel für ungerade Werte nutzen, nämlich (n+1)/2, also (11+1)/2 = 6.
Natürlich ist nicht 6 unser Median, sondern der sechstgrößte Wert, also Clotilde mit 3,50 Euro (unsere Daten sind ja sortiert, sonst geht das nicht so schön).
Quartile in Excel berechnen
Unser 1. Quartil ist ja wiederum die Hälfte der unteren Hälfte. Also teilen wir noch einmal durch zwei. Oder anders ausgedrückt: Wir teilen die Zahl durch 4 statt durch 2. Unsere Formel für das 1. Quartil ist also (11+1)/4 = 3.
Für den zweiten und dritten Wert multiplizieren wie die Position jetzt einfach mit 2 oder 2. Das zweite Quartil (Median) ist also der sechste, das dritte der neunte Wert. Also 3,50 Euro und 5,- Euro.
Die Formel allgemein formuliert
Für unterschiedliche Quantile lautet die Rechenformel, die hinter den Excel-Formeln mit dem Zusatz .exkl steht also
(n+1)/z*q
Dabei ist
- n = die Fallzahl, in unserem Fall also 11,
- z = die Zahl der Gruppen, bei Quartilen also 4, bei Perzentilen 100 und so weiter,
- q = das Quantil, also 1 für das erste Quantil, 2, für das zweite und so weiter. Wollen wir das dritte Quartil wissen, müsste hier eine 3 stehen.
Nicht vergessen: Das Ergebnis gibt die Position unseres Quantil an, wir müssen bei der Rechnung von Hand erst in der Liste nachsehen. Rechnen wir mit Excel, wird uns direkt der Wert angegeben. Für Excel müssen wir die Daten auch nicht sortieren, das macht Excel selbst.
Jetzt bleiben noch zwei Fragen: Was macht Excel, wenn es nicht so schön aufgeht und wie rechne ich bei geraden Zahlen.
Was, wenn das Ergebnis eine Kommazahl ist?
Natürlich habe ich das Beispiel mit elf Werten ausgesucht, weil (11+1)/4 genau 3 ergibt. Was aber, wenn wir beispielsweise 13 Werte hätten? Dann ist unser Ergebnis (13+1)/4 = 3,5.
| lfd. Nr. | Name des Kindes | Taschengeld |
| 1 | Hans | 0,- |
| 2 | Hermine | 0,- |
| 3 | Xaver | 1,- |
| 4 | Beat | 2,- |
| 5 | Hildegard | 3,- |
| 6 | Clotilde | 3,50 |
| 7 | Tusnelda | 4,- |
| 8 | Ambrosius | 4,- |
| 9 | Sigismund | 5,- |
| 10 | Helene | 7,- |
| 11 | Gesine | 8,- |
| 12 | Gisbert | 9,- |
| 13 | Marianne | 10,- |
Die Antwort liegt auf der Hand, wir nehmen einfach die Mitte aus dem 3. und dem 4. Wert. Oder anders ausgedrückt: Wir berechnen die Differenz vom 3. zum 4. Wert, multiplizieren sie mit 0,5 und addieren das Ergebnis zum dritten Wert. Diese zweite Betrachtungsweise hat den Vorteil, dass sie analog auch für alle anderen Kommazahlen funktioniert.
Am Beispiel oben: Unser dritter Wert ist Xaver mit 1,- Euro Taschengeld, der vierte Beat mit 2,- Euro. Die Mitte zwischen beiden ist 1,50 Euro. Hätten wir Quintile, wäre unser erstes Quintil (13+1)/5 = 2,8. Dann müssen wir den zweiten, etwas umständlicheren Berechnungswert wählen. Wir nehmen den 2. Wert, weil unsere Zahl vor dem Komma die 2 ist, also 0,- Euro. Hinter dem Komma steht eine 0,8, daher nehmen wir die Differenz zum nächstgrößeren Wert und rechnen sie mal 0,8. Weil der nächstgrößere Wert 1,- Euro ist und die Differenz von 0,- Euro zu 1,- Euro – wie jeder ziemlich leicht ausrechnen kann – genau 1,- Euro, rechnen wir 0,- Euro + (1,- Euro * 0,8), was 0,80 Euro ist. Unser erstes Quintil ist also 0,8.
Kleiner Test in Excel mit der Formel =QUANTIL.EXKL(A2:A14;1/5) für unsere Qunitilsberechnung: Excel kommt zum gleichen Ergebnis.
Die weiteren Werte sind ganz einfach zu bestimmen, sie sind immer Vielfache. Für das 1. Quartil haben wir 3,5 (also die Mitte aus dem 3. und dem 4. Wert), dann bekommen wir für das 2. Quartil genau den 7. Wert (=2*3,5) und für das 3. Quartil 3*3,5 =10,5 – also die Mitte aus dem 10. und dem 11. Wert.
Wie funktioniert das bei geraden Zahlen?
Das funktioniert analog für jede andere Kommazahl. Beim Median haben wir ja bekanntlich für eine gerade Zahl von Fällen eine andere Formel. Statt (n+1)/2 rechnen wir dort mit n/2 den Untermedian aus und mit n/2 + 1 den Obermedian.
Aber das stört uns nicht, denn wenn wir bei Kommazahlen wie soeben erklärt vorgehen, kommen wir genau zum gleichen Ergebnis. Wenn wir bei 100 Werten (100+1)/2 rechnen kommen wir auf 50,5. Nehmen wir nun den 50. Wert und addieren noch 0,5 * die Differenz zum 50. zum 51. Wert erhalten wir das gleiche Ergebnis, wie wenn wir n/2 = 50 rechnen und dann das arithmetische Mittel aus diesem Wert und dem n/2 + 1 = 51. Wert nehmen.
Die Formeln quantil.inkl und quartile.inkl
Wie gesagt bekommen wir bei der oben stehenden Berechnung und mit der Formel quartile.exkl(…;1) auf einen Wert von 1,50 Euro für das erste Quartil. Mit der Formel quartile.inkl(…;1) ist unser Ergebnis dagegen 2,- Euro, also genau der vierte Wert. Der Median liegt ebenfalls bei 4,- Euro, der 3. Quartilswert weicht wieder ab, er liegt jetzt bei 7,- Euro, dem 10. Wert.
| lfd. Nr. | Name des Kindes | Taschengeld |
| 1 | Hans | 0,- |
| 2 | Hermine | 0,- |
| 3 | Xaver | 1,- |
| 4 | Beat | 2,- |
| 5 | Hildegard | 3,- |
| 6 | Clotilde | 3,50 |
| 7 | Tusnelda | 4,- |
| 8 | Ambrosius | 4,- |
| 9 | Sigismund | 5,- |
| 10 | Helene | 7,- |
| 11 | Gesine | 8,- |
| 12 | Gisbert | 9,- |
| 13 | Marianne | 10,- |
Wie rechnet Excel bei quartile.inkl(;)?
Diese Formel für quartile.inkl(;) ist etwas komplizierter, aber auch eigentlich logisch. Wir wollen ja, dass ein Viertel der Werte unterhalb des ersten Quartilswertes liegt und drei Viertel darüber. Die Quartilsgrenze selbst zählt nicht mit. Wir müssen bei 13 Werten also 12 Werte in vier Gruppen aufteilen. Also teilen wir n-1 durch 4 statt n+1. Allerdings brauchen wir die Grenze wieder, darum addieren wir sie später wieder dazu, also
(n-1)/4+1
Bei 13 Werten ist die Berechnung also (13-1)/4+1, also der 4. Wert. Für den 2. und 3. Wert multiplizieren wir jetzt – wie schon bei den .exkl-Formeln – alles mit 2 und 3, aber bevor wie +1 rechnen.
Wir rechnen für das dritte Quartil also
(n-1)/4*3+1.
Das ergibt (13-1)/4*3+1 = 12/4*3+1 = 3+3+1 = 9+1 = 10.
Oder etwas allgemeiner ausgedrückt
(n-1)/z*q+1
wobei gilt
n = Anzahl der Fälle
z = Anzahl der Gruppen in die wir unterteilen, also bei Quartilen 4
qp = die Postion unseres Quantils, suchen wir das 3. Quantil also 3
Funktioniert das bei allen Zahlen?
Vielleicht werden jetzt manche einwenden, dass sich meine Argumentation ja auf einen Fall stützt, wo es auch tatsächlich eine Grenze gibt. Genau der 4. Wert ist meine Quartilsgrenze. Aber geht das auch, wenn wir beispielsweise 9 Werte haben? Oder statt mit Quartilen mit Quintilen rechnen?
Ich habe es ausprobiert, die Formel kommt auch dort auf das gleiche Ergebnis wie die Excel-Formel =quantil.inkl(;). Aber das nur als Hintergrundwissen. Für die meisten wird es reichen zu wissen, wann sie welche Formel anwenden.
Deshalb hier noch mal kurz zusammengefasst:
quartile.exkl(;) und quantil.exkl(;) nutze ich, wenn ich möglichst gleich große Gruppen bilden will.
quartile.inkl(;) und quantil.inkl(;) nutze ich, wenn ich Aussagen treffen will wie „Das oberste 1,0 Prozent verfügt über …Prozent des Vermögens“. Üblicher ist die Berechnung mit .inkl.
Und natürlich muss ich bei den beiden Formel mit quantil noch angeben, welches quantil ich verwende, indem ich hinter dem Strichtpunkt einen Bruch schreibe, bei dem oben das Quantil steht (zum Beispiel das 99.) und und unten die Zahl der gebildeten Gruppen (zum Beispiel 100), für das 99. Perzentil als 99/100.
Schreiben Sie einen Kommentar